本文不讨论二叉树层次遍历

刷题的时候看到一些二叉树遍历的解法，整理在这里作为笔记，也分享给大家

语言是 Java 的，我会采取代码+图解+说明形式来尽可能讲明白每种遍历方式

一些准备

为了便于整理和展示，我建立了一个简单的纯 Java 工程来测试各种解法

树节点类代码（TreeNode）

一个简单的树节点类：

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

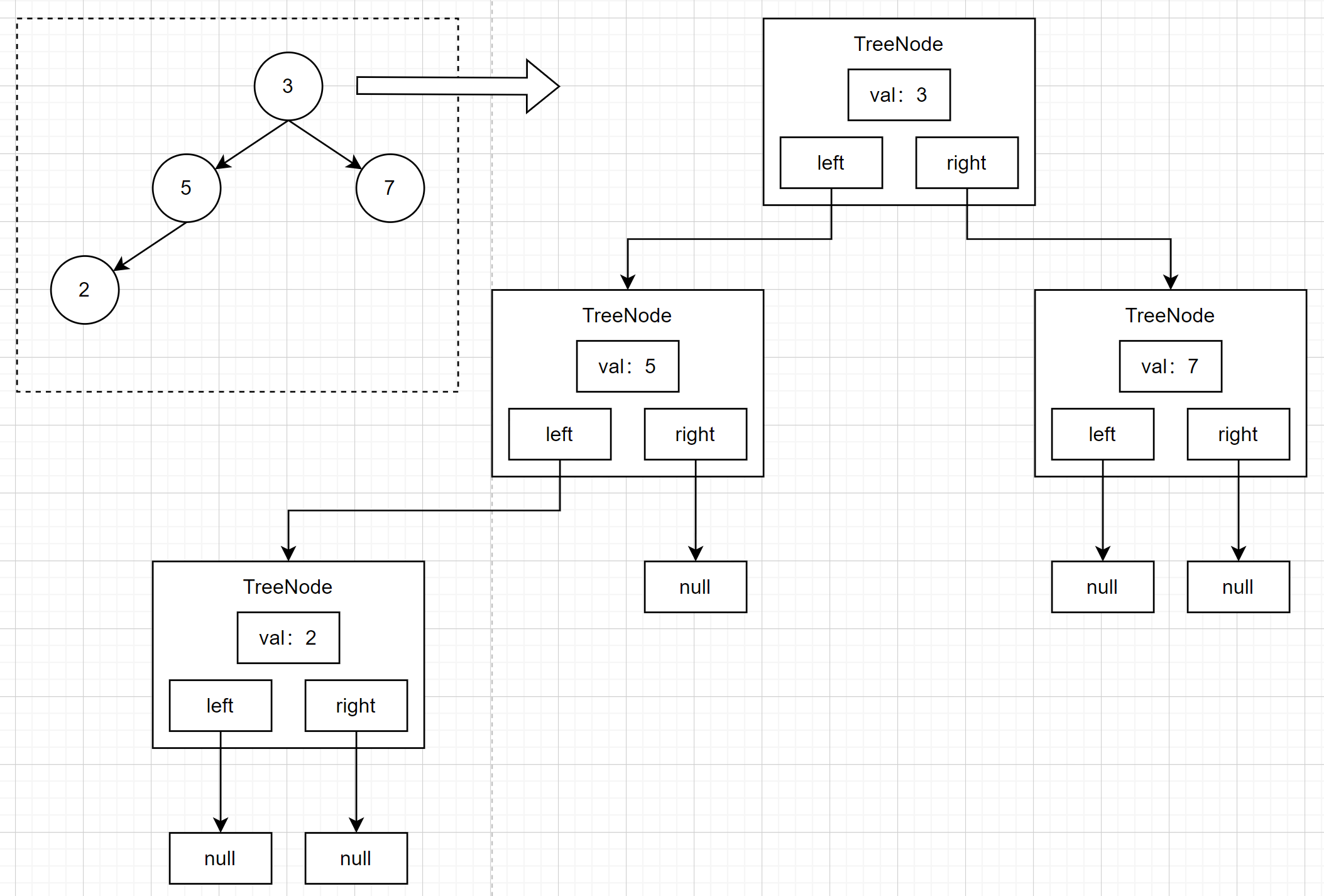
树节点类图解

这是一棵二叉树，它拥有四个树节点，左侧虚线框内是它的简化图

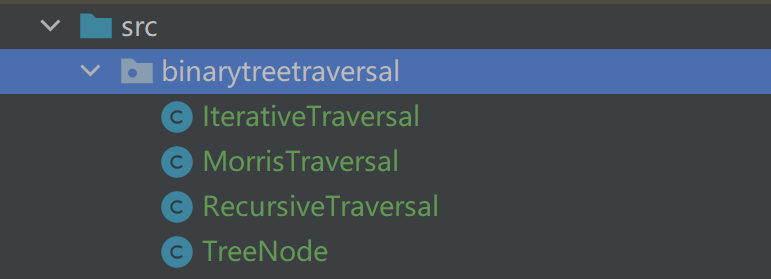
工程文件结构

工程文件说明

• TreeNode：树节点类
• RecursiveTraversal：递归遍历二叉树的各种实现
• IterativeTraversal：迭代遍历二叉树的各种实现
• MorrisTraversal：Morris 遍历二叉树的各种实现

递归解法（RecursiveTraversal）

• 二叉树天然是一种递归结构，因此递归解法是最简洁的，代码量最少
  • 简洁不一定可读性好；对于不熟悉递归思想的人来说，递归解的可读性并不高
• 显而易见，递归解法总是会消耗大量栈空间
  • 而且，Java 编译器不支持尾递归优化（这与 Java 语言的设计哲学和实现细节有关）
• 另一方面，递归导致的大量函数调用，会产生一定不必要的开销

递归解法复杂度

时间复杂度	空间复杂度
O(n)	O(n)

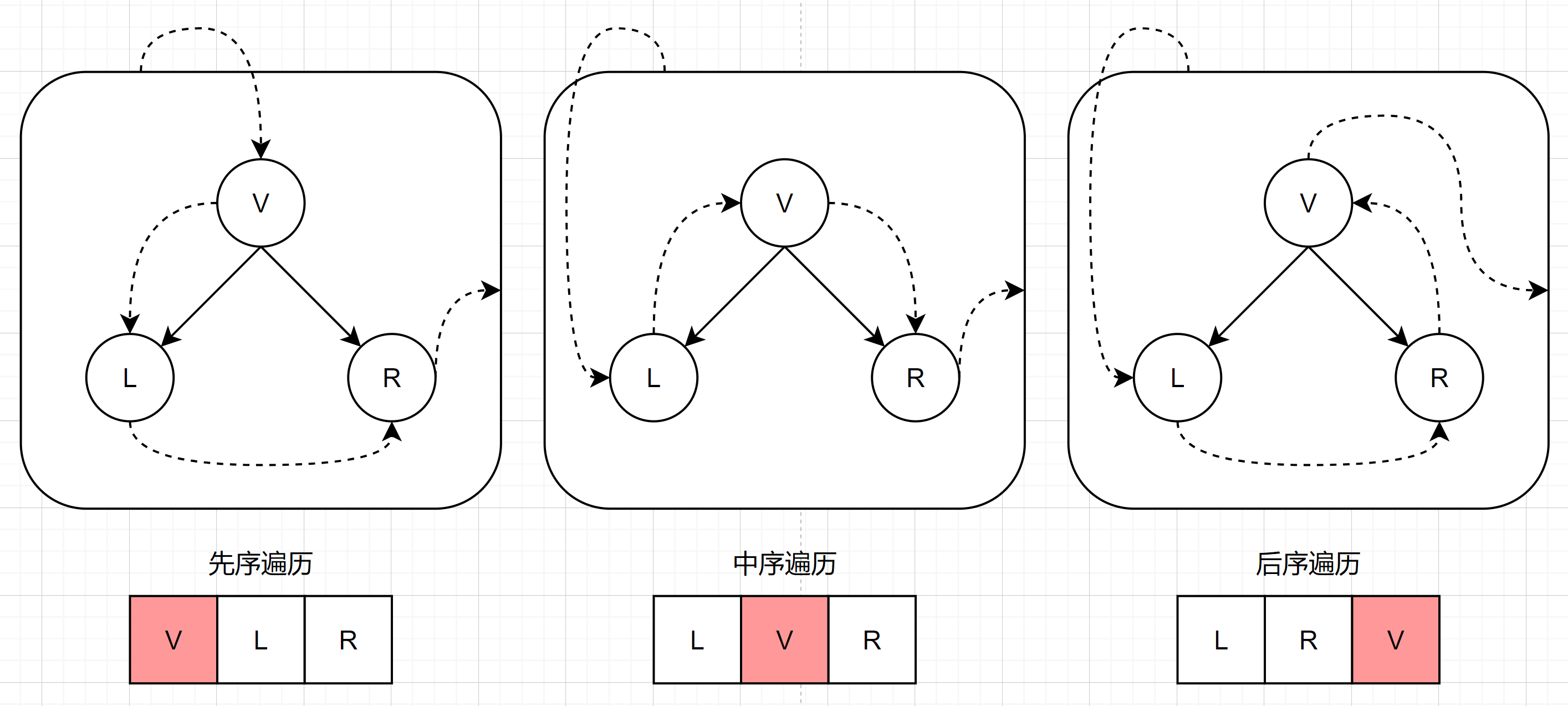
前序（递归）

根左右

public static void preOrder(TreeNode root) {
    if (root == null) return;

    System.out.print(root.val + " ");
    preOrder(root.left);
    preOrder(root.right);
}

中序（递归）

左根右

public static void inOrder(TreeNode root) {
    if (root == null) return;

    inOrder(root.left);
    System.out.print(root.val + " ");
    inOrder(root.right);
}

后序（递归）

左右根

public static void postOrder(TreeNode root) {
    if (root == null) return;

    postOrder(root.left);
    postOrder(root.right);
    System.out.print(root.val + " ");
}

迭代解法（IterativeTraversal）

• 使用辅助数据结构（自定义栈）代替系统栈，有效降低栈空间消耗和溢出风险
• 避免了大量函数调用所产生的开销
• 代码复杂度相对较高
  • 然而，这并不意味着迭代解法更难以理解

迭代解法复杂度

时间复杂度	空间复杂度
O(n)	O(n)

前序（迭代，单层循环）

需要区分的一点是：

• 递归中，进入的是子树
• 迭代中，压入的是节点

尽管子树和节点看起来都是一个 TreeNode，但它们之间存在一些区别！

另外，这里使用 LinkedList（双向链表），而非 Stack

因为 Stack 底层是基于数组实现的，对于频繁插入和删除的场景下，并不太适合

注意：选择数组或链表实现栈的优劣取决于二叉树的分布特点

对于单层循环方式，我们利用栈的后进先出特点，要先压入右子节点，再压入左子节点

public static void preOrder1(TreeNode root) { // 前序单层循环
    if (root == null) return;

    Deque<TreeNode> stack = new LinkedList<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        System.out.print(node.val + " ");
        if (node.right != null) stack.push(node.right);
        if (node.left != null) stack.push(node.left);
    }
}

前序（迭代，双层循环）

内循环中压入子树的所有左子节点

public static void preOrder2(TreeNode root) { // 前序双层循环
    if (root == null) return;

    TreeNode node = root;
    Deque<TreeNode> stack = new LinkedList<>();
    while (!stack.isEmpty() || node != null) {
        while (node != null) {
            System.out.print(node.val + " ");
            stack.push(node);
            node = node.left;
        }
        node = stack.pop();
        node = node.right;
    }
}

中序（迭代，双层循环）

对于单层循环方式，我们必须先把根节点压入栈中，所以它无法实现中序遍历

内循环中压入子树的所有左子节点

public static void inOrder(TreeNode root) { // 中序双层循环
    if (root == null) return;

    TreeNode node = root;
    Deque<TreeNode> stack = new LinkedList<>();
    while (!stack.isEmpty() || node != null) {
        while (node != null) {
            stack.push(node);
            node = node.left;
        }
        node = stack.pop();
        System.out.print(node.val + " ");
        node = node.right;
    }
}

后序（迭代，单层循环）

对于单层循环方式，后序遍历可以采用一个讨巧的办法：逆序输出

这需要额外的开销（对于下面的代码，既有辅助栈的空间开销，也有逆序的时间开销）

public static void postOrder1(TreeNode root) { // 后序单层循环
    if (root == null) return;

    Deque<TreeNode> stack1 = new LinkedList<>();
    Deque<TreeNode> stack2 = new LinkedList<>();
    stack1.push(root);
    while (!stack1.isEmpty()) {
        TreeNode node = stack1.pop();
        stack2.push(node);
        if (node.left != null) stack1.push(node.left);
        if (node.right != null) stack1.push(node.right);
    }
    while (!stack2.isEmpty()) {
        System.out.print(stack2.pop().val + " ");
    }
}

后序（迭代，双层循环）

内循环中压入子树的所有左子节点

public static void postOrder2(TreeNode root) { // 后序双层循环
    if (root == null) return;

    TreeNode node = root;
    TreeNode prev = null;
    Deque<TreeNode> stack = new LinkedList<>();
    while (!stack.isEmpty() || node != null) {
        while (node != null) {
            stack.push(node);
            node = node.left;
        }
        node = stack.pop();
        if (node.right == null || node.right == prev) {
            System.out.print(node.val + " ");
            prev = node;
            node = null;
        } else {
            stack.push(node);
            node = node.right;
        }
    }
}

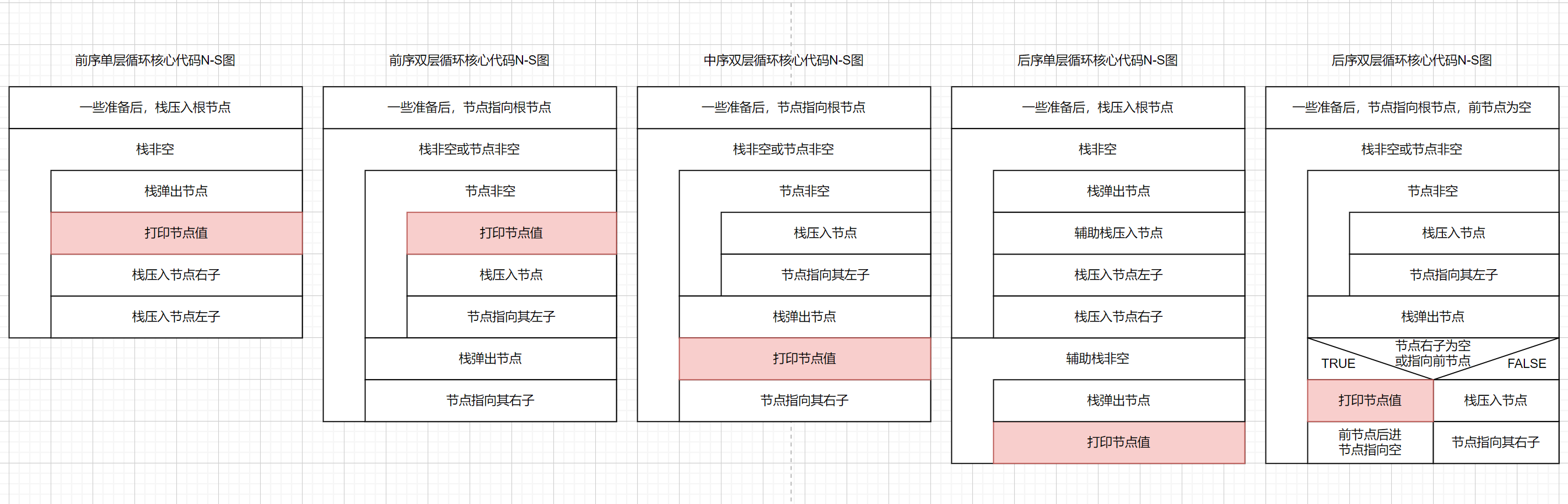
5种迭代解法图解

我绘制了5种解法的核心代码 N-S 图，以便于横向对比

Morris 解法（MorrisTraversal）

• 本质上，Morris 解法利用了二叉树节点中指向 null 的 left 和 right 属性（空闲指针），将原本的二叉树改造成临时线性结构，从而实现空间复杂度 O(1) 的遍历
• 在传统的线索二叉树中，我们一般需要使用左右 tag 来标识指向的是左右节点还是前驱或后继节点；Morris 解法可以看作是一种不使用 tag 的线索化二叉树方法
• Morris 解法不能直接适用于后序遍历，需要额外的操作才能实现（本文不展示）
• Morris 解法在遍历过程中修改了树的结构，因此不是线程安全的

Morris 解法复杂度

时间复杂度	空间复杂度
O(n)	O(1)

前序（Morris）

public static void preOrder(TreeNode root) {
    if (root == null) return;

    TreeNode cur1 = root;
    TreeNode cur2 = null;
    while (cur1 != null) {
        cur2 = cur1.left;
        if (cur2 != null) {
            // 找到左子树的最右叶子节点
            while (cur2.right != null && cur2.right != cur1) {
                cur2 = cur2.right;
            }
            if (cur2.right == null) {
                cur2.right = cur1;
                System.out.print(cur1.val + " ");
                cur1 = cur1.left;
                continue;
            } else {
                cur2.right = null;
            }
        } else {
            System.out.print(cur1.val + " ");
        }
        cur1 = cur1.right;
    }
}

中序（Morris）

public static void inOrder(TreeNode root) {
    if (root == null) return;

    TreeNode cur1 = root;
    TreeNode cur2 = null;
    while (cur1 != null) {
        cur2 = cur1.left;
        if (cur2 != null) {
            // 找到左子树的最右叶子节点
            while (cur2.right != null && cur2.right != cur1) {
                cur2 = cur2.right;
            }
            if (cur2.right == null) {
                cur2.right = cur1;
                cur1 = cur1.left;
                continue;
            } else {
                cur2.right = null;
            }
        }
        System.out.print(cur1.val + " ");
        cur1 = cur1.right;
    }
}